La Gran Pirámide y la Tierra
LA GRAN PIRÁMIDE DE KEOPS [Khufu]
El número 432 y las medidas de la Tierra
El número 432 lo encontraremos repetidamente asociado a la Gran Pirámide. Era un número popular en Oriente, y es igual a 6 x 6 x 6 x 2, por lo que se halla asociado al sistema sexagesimal.
El primer hallazgo que permitió la reconstrucción de la Gran Pirámide fue que el ángulo de inclinación exacto que formaba con su base era de 51,84º. Por tanto, si multiplicamos 51,84º por los 60′ de cada grado y por los 60″ de cada minuto de arco, obtendremos 186.624 segundos de arco. Y esta cifra es igual a 432 al cuadrado (4322).
El número 432 asociado a la Gran Pirámide se transformaría en la proporción clave entre las medidas de la Gran Pirámide y las dimensiones de la Tierra.
Porque a partir de la reconstrucción informática del modelo original del monumento se puede afirmar, sin ninguna duda, que algunas de las longitudes de la Gran Pirámide escondían proporciones con las dimensiones de la Tierra a través del número 432.
Esta igualdad entre el pletro y el segundo de arco del perímetro medio de la Tierra era un hecho hasta hoy desconocido.
6 pletros formaban 1 estadio (185,325 m) —una unidad de longitud llamada estadio olímpico en Grecia—. En consecuencia, 1 estadio sería la medida de 1 / 10 parte de 1 minuto de arco (1.853,249 m) del perímetro medio de la Tierra.
Por tanto, el sistema de medidas sexagesimal que ha llegado hasta nosotros desde la antigüedad a través del pletro [1] y del estadio, demuestra algo inesperado…
Figura 21. La relación entre la Gran Pirámide y las medidas de la Tierra. En la parte superior se puede observar la apotema remarcada en rojo sobre la pirámide. En la parte inferior sobre ambas esferas se han dibujado: en línea discontinua, el ecuador; en negro, el meridiano; y en rojo, el perímetro medio de la Tierra.
¡Las medidas de la Tierra ya se conocían en el Antiguo Egipto y en la Grecia clásica! [2]
Recordemos que la apotema es la altura de las caras triangulares de una pirámide (fig. 21).
Si la apotema de la Pirámide mide 1 estadio, eso significa que el perímetro medio de la Tierra puede obtenerse a partir de la Gran Pirámide, con una aproximación del 99,994%. ¿Cómo? Multiplicando la apotema alargada hasta el suelo por la mitad de 432.000 [2].
Y esta longitud puede obtenerse con una aproximación del 99,997%, al multiplicar el perímetro total del zócalo de la Gran Pirámide por la mitad de 43.200 (fig. 21).
El número 432 nos ayuda, pues, a proporcionar las longitudes de la Gran Pirámide con las dimensiones de nuestro planeta. Y esta sorprendente utilidad aún se manifestará de forma más precisa a través de una nueva proporción entre la Gran Pirámide y el meridiano terrestre.
Por tanto, el perímetro del meridiano terrestre puede obtenerse con una aproximación del 99,999%, al multiplicar el perímetro del zócalo de la Gran Pirámide en contacto con el suelo por 43.200 (fig. 21).
Esa doble relación entre el zócalo y la Tierra nos revela su excepcional función simbólica: el zócalo, el elemento de contacto entre la Gran Pirámide y la Tierra, a través de sus medidas y con la colaboración del número 43.200, nos ofrece las proporciones entre el monumento y el planeta, y nos permite obtener, a la vez, el perímetro medio de la Tierra y la longitud del meridiano terrestre.
La relevancia y la magia matemática del número 432 se manifiesta, pues, en las longitudes de la Gran Pirámide porque nos permiten calcular las dimensiones de la Tierra.
A través de las longitudes de la Gran Pirámide y mediante múltiplos del número 432, sus sacerdotes-arquitectos, establecieron proporciones que nos permiten deducir el meridiano terrestre, el perímetro medio de la Tierra y el radio polar del planeta.
Una latitud sorprendente
La repetida presencia del número 43.200 como proporción entre la Gran Pirámide y la Tierra lo transforma en un número del espacio.
No obstante, el 43.200 también es un número popular porque lo llevamos con nosotros. ¿Sabes dónde?
Tú, yo y millones de hombres y mujeres de todo el planeta llevamos el número 43.200 oculto en nuestros relojes de pulsera. Porque 43.200 son los segundos de 12 horas.
Los diseñadores de la Gran Pirámide parecen insistir, pues, en la idea de números comunes al espacio y al tiempo, por lo que hemos de preguntarnos…
¿A través del número 43.200 los sacerdotes-arquitectos de la Gran Pirámide quisieron explicarnos que conocían el concepto de espacio-tiempo?
Cabe recordar que la idea de espacio-tiempo es un importantísimo avance de la física contemporánea, desarrollado mediante su teoría de la relatividad por Albert Einstein.
Al respecto, hay que señalar que la latitud de la Gran Pirámide, de 29º 58’ 45,02” N, nos ofrece un dato realmente sorprendente. Al expresar la latitud del monumento en el sistema decimal es igual a 29,9791722º N, un número en diezmilésimas de grado resulta ser 299.791,722. Y la velocidad de la luz en km/s es, nada más y nada menos, 299.792,458.
El nivel de precisión es de un 99,9998% Y la desviación de ese cálculo respecto del centro de la Gran Pirámide es de –8,2 m, cuando el error de cálculo del sistema GPS es de entre 5 y 10 m. Por tanto, como con este nivel de precisión es imposible que se trate de una relación casual, resulta una evidencia revolucionaria:
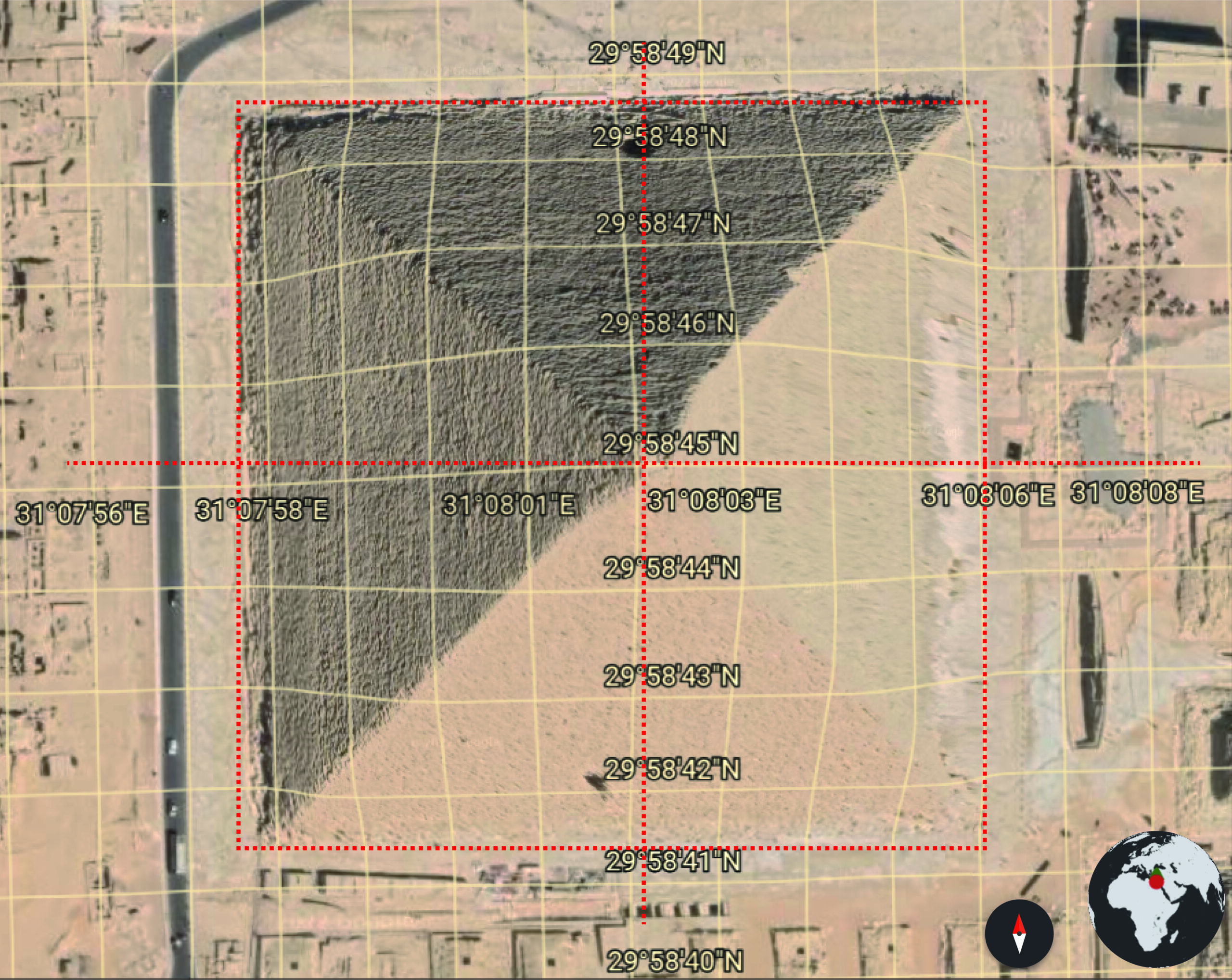
Figura 22. La latitud de la Gran Pirámide, según el programa Google Earth.
¡La latitud de la Gran Pirámide en diezmilésimas de grado es igual a la velocidad de la luz en km/s!
Este descubrimiento expuesto en la tesis doctoral del Dr. Pérez-Sánchez, ya ha sido recogido en diversos documentales.
Al paralelo de 29,9792458º N que pasa sobre la Gran Pirámide muy cerca de su centro, lo llamaremos el Paralelo de la Luz.
La velocidad de la luz no fue establecida con exactitud por la física contemporánea hasta bien entrado el siglo XX.
Por tanto, surge un nuevo interrogante:
Un meridiano objetivo para la Tierra
Hemos visto hasta ahora que del análisis del modelo original de la Gran Pirámide se puede deducir el conocimiento de la esfericidad y de las medidas de la Tierra.
Si los sacerdotes-arquitectos de la Gran Pirámide la hubieran situado en el Paralelo de la Luz significaba que habían podido ubicar exactamente el ecuador terrestre, ya que es a partir de él que se mide la latitud: de 0 a +90º de latitud Norte y de 0 a –90º de latitud Sur, correspondiendo los 0º a la latitud del ecuador, y los 90º Norte o los 90º Sur a la latitud de los polos.
La determinación del Meridiano de Greenwich como primer meridiano de longitud 0º es una convención establecida en la Conferencia Internacional de Washington (1884). Por tanto, hemos de preguntarnos:
Una posibilidad sería hacer pasar el meridiano terrestre por una cima muy importante o de gran significado simbólico. Entonces, en el caso de que una civilización científica hubiera conocido la totalidad de la Tierra, esa cima podría haber sido su máxima altura: el Monte Everest. Y a pesar de que no fue reconocido como el techo de la Tierra hasta bien entrado el siglo XX, esta sería la solución. Veámoslo.
DEF monte everest-01
Figura 23. Las coordenadas del Monte Everest, según el programa Google Earth.
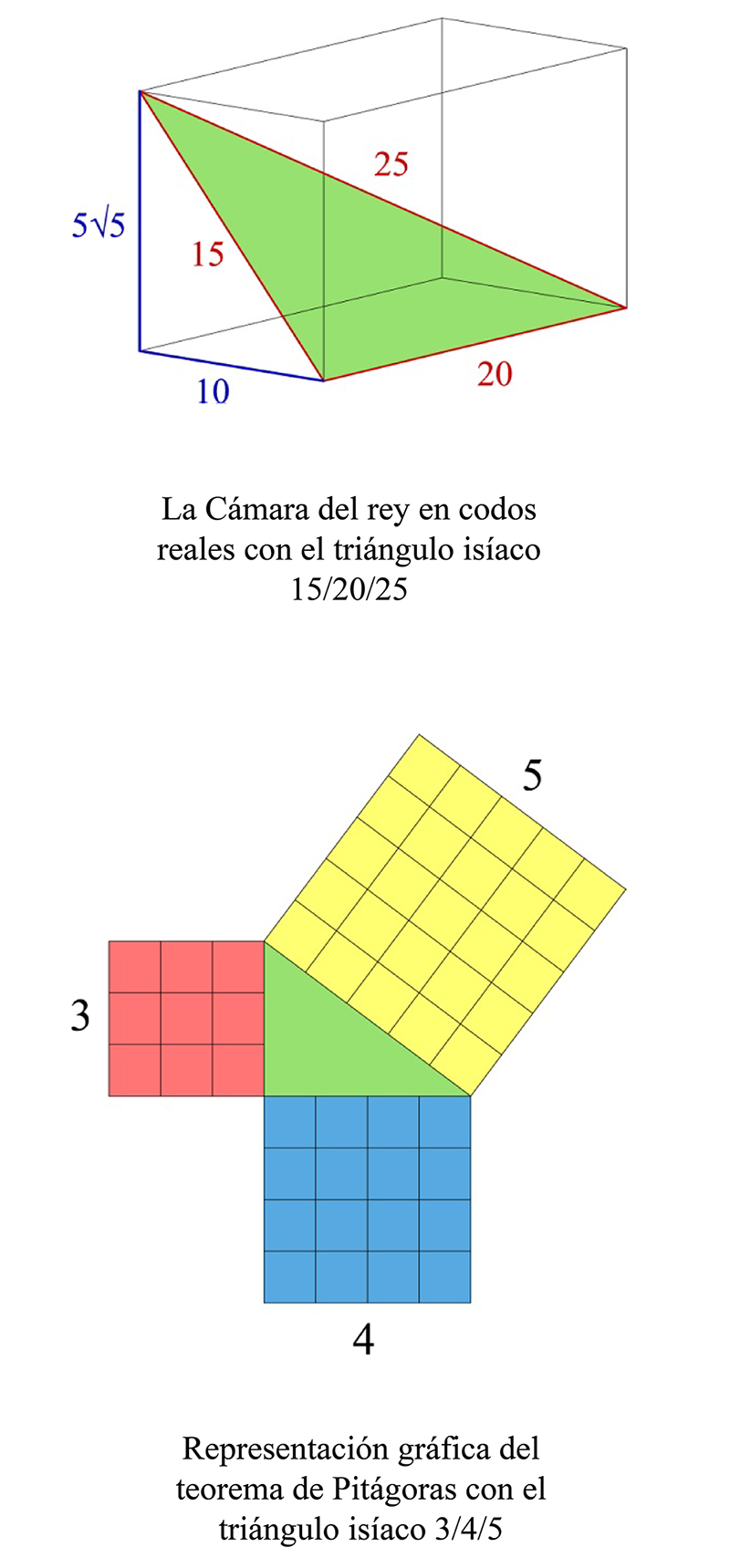
Figura 24. A. La Cámara del Rey y el Teorema de Pitágoras: 152 + 202 = 252. B. Representación gráfica del Teorema de Pitágoras como suma de superficies: 32 + 42 = 52.
Las coordenadas del Monte Everest son 27º 59’ 18,09” N y 86º 55’ 30,73” E, que en el sistema decimal resultan ser 27,988358º N y 86,925203º E.
Como la medida del meridiano es 40.007,832 km, y la del ecuador, 40.075,017 km, y como la distancia entre meridianos, medida sobre los paralelos, es proporcional al coseno de la latitud, resulta que las coordenadas de la Gran Pirámide referidas al ecuador y al meridiano del Monte Everest, expresadas en un número entero de km, serían: latitud norte 3.332 km, longitud oeste 5.380 km [4].
Estos dos números forman una terna pitagórica, ya que 5.3802 – 3.3322 = 4.2242.
Las ternas pitagóricas son series de tres números enteros que —como en el caso del 3.332, el 4.224 y el 5.380— cumplen el Teorema de Pitágoras: a2 + b2 = c2, es decir, 3.3322 + 4.2242 = 5.3802. Y las ternas pitagóricas son enormemente difíciles de obtener.
Un ejemplo clásico de terna pitagórica es 3, 4 y 5, ya que 32 + 42 = 52. Otro ejemplo es 5, 12 y 13, ya que 52 + 122 = 132. Y por extraño que parezca, ambas ternas se hallan en el interior de la Gran Pirámide: la primera, en la Cámara del Rey; y la segunda, en la Cámara de la Reina.
Porque los antiguos egipcios habían de ser maestros en agrimensura, el arte de medir las tierras, ya que cada año, después de la crecida del Nilo, habrían de volver a marcar los límites entre propiedades. Y el Teorema de Pitágoras lo que geométricamente nos ofrece es una suma de superficies.
Es prácticamente imposible, pues, que sea casualidad el hecho que las coordenadas geográficas de la Gran Pirámide estén relacionadas mediante una terna pitagórica formada por números de cuatro cifras.
Y más, aún, si los números que determinan la latitud y la longitud de la Gran Pirámide (3.332 y 5.380) pueden obtenerse mediante la diferencia y la suma de los dos mismos cuadrados, ya que se cumple, a la vez, 3.332 = 662 – 322, y también, 5.380 = 662 + 322.
Esta serie de asociaciones matemáticas entre las coordenadas geográficas de la Gran Pirámide, el Teorema de Pitágoras y las ternas pitagóricas, por cálculo de probabilidades es imposible que sea casual. Por tanto,
Los sacerdotes-arquitectos de la Gran Pirámide la situaron respecto de un sistema de coordenadas geográficas referido al ecuador y a un meridiano 0 que pasaba por la cima del Monte Everest.
Las coordenadas de la Gran Pirámide son 29º 58’ 45,02” N y 31º 08’ 03,14” E, y las del Monte Everest, 27º 59’ 18,09” N y 86º 55’ 30,73” E. Al cambiar el meridiano de referencia cambiará la longitud geográfica de la Gran Pirámide.
Entonces la diferencia de longitudes geográficas entre la Gran Pirámide y el Monte Everest nos dará la longitud objetiva de la Gran Pirámide referida al meridiano 0 del Monte Everest: 86º 55′ 30,73″ – 31º 08′ 03,14″ = 55º 47′ 27,59″ Oeste = 55,790997º Oeste. Y esta medida, con una aproximación del 99,993% equivale al perímetro de una circunferencia que tuviera de radio ¡8,88º!
Ante esta suma de evidencias, nacen nuevos interrogantes:
Figura 25. El meridiano 0 objetivo pasaba por el Monte Everest.
Figura 25. El meridiano 0 objetivo pasaba por la cima del Monte Everest.
Los sacerdotes-arquitectos de la Gran Pirámide, ¿cómo pudieron saber que el Monte Everest era la cima más alta del planeta?
¿Qué era o qué representaba el número 888 que se hallaba asociado al espacio, al tiempo, y a la longitud geográfica de la Gran Pirámide?
¿Cuál podría ser la procedencia de ese saber científico y enciclopédico que vamos descubriendo al estudiar la Gran Pirámide de Keops?
[1] Estas relaciones métricas que se incluyen en la tesis doctoral La Gran Pirámide, clave secreta del pasado (UPC, 2007), coinciden con las observaciones que Mario Ruiz Morales, profesor Doctor de la Universidad de Granada e ingeniero geógrafo del Ministerio de Fomento, ha publicado en su libro Metrología histórica en la Descripción de Egipto, Editorial Universidad de Granada, 2011.
[2] La longitud de 1 segundo de arco resulta de dividir el perímetro medio de la Tierra por sus 360º, por los 60′ de cada grado, y por los 60″ de cada minuto. Por tanto, 1 segundo de arco o pletro será igual al perímetro medio de la Tierra dividido por 1.296.000 (igual a 360 x 60 x 60). Entonces 1 estadio será 6 veces mayor, es decir, será igual al perímetro medio de la Tierra dividido por 216.000, una cifra igual a la mitad de 432.000.
[3] Tomemos el perímetro del meridiano terrestre, de 40.007,832 km y sigamos el mismo proceso anterior. Si lo dividimos en 360 partes obtendremos la longitud de 1º, y si subdividimos cada grado en 60 partes, resultará la medida de 1′, que coincide con la definición de la milla náutica. Su longitud será de 1.852,214 m
[4] Las coordenadas de la Gran Pirámide son 29º 58’ 45,02” N y 31º 08’ 03,14” E, y las del Monte Everest, 27º 59’ 18,09” N y 86º 55’ 30,73” E. Por lo tanto, como los 360º del meridiano miden 40.007,832 km, aplicando una sencilla regla de tres, la distancia de la Gran Pirámide al ecuador resulta ser: 40.007,832 x 29,979172º / 360º = 3.331,671 km, una cifra que expresada en números enteros corresponde a 3.332 km de latitud —no obstante, los sabios egipcios no consideraron que la medida de 1° es menor en el ecuador que en el polo, por lo que la distancia de un punto de la Tierra al ecuador no es exactamente proporcional a su latitud—. En el cálculo de la longitud geográfica hay que considerar que las distancias medidas sobre el paralelo entre meridianos, disminuyen con la proximidad al polo proporcionalmente al coseno de la latitud, ya que los meridianos se acercan entre sí al acercarse al polo. La diferencia de coordenadas entre la Gran Pirámide y el Monte Everest es la siguiente: 86º 55′ 30,73″ – 31º 08′ 03,14″ = 55º 47′ 27,59″ = 55,790997º que en realidad disminuye al multiplicarla por el coseno de la latitud de la Gran Pirámide: 55,790997º x coseno 29,979172º = 48,326558º. Esta medida, sobre los 360º del ecuador que mide 40.075,017 km, representan 40.075,832 x 48,326558º / 360º = 5.379,688 km, una cifra que expresada en números enteros corresponde a 5.380 km de longitud geográfica. Por tanto, las coordenadas de la Gran Pirámide así calculadas y expresadas en un número entero de km respecto del ecuador y del meridiano del Everest serían: latitud 3.332 km, longitud 5.380 km.
[5] 8,88º = 8,88 x 60′ = 532,8′. Y como que 1 minuto de arco es igual a 10 estadios, 532,8 x 10 estadios = 5.328 estadios.